Next: Riskfactor.help, Previous: Debt.help, Up: Octave octarisk Classes [Contents][Index]
Class for setting up Sensitivity objects. This class contains two different instrument setups. The first idea of this class is to model an instrument whose shocks are derived from underlying risk factor shocks or idiosyncratic risk (for MC only). The shocks from these risk factors are then applied to the instrument base value under the assumption of a Geometric Brownian Motion or Brownian Motion. Basically, all real assets like Equity or Commodity can be modelled with this class. The combined shock is a linear combination of all underlying risk factor shocks:
V_shock = V_base * exp(Sum_i=1...n [dRF_i * w_i]) (Model: GBM) V_shock = V_base + (Sum_i=1...n [dRF_i * w_i]) (Model: BM)
with the new shock Value V_shock, base V_base, risk factor shock dRF_i and risk factor weight w_i.
The second idea is to use this class to specify a polynomial function or taylor series of underlying instruments, risk factors, curves, surfaces or indizes and derive the sensitivity value with the following formulas. If Taylor expansion shall be used:
V_shock = V_base + a1/b1 * x1^b1 + a2/b2 * x2^b2 + .. + an/bn * xn^bn * am/bm * xm^bm
The base value is used only if appropriate flag is set. Otherwise, a polynomial function can be set up:
V_shock = V_base + a1 * x1^b1 + a2 * x2^b2 + .. + an * xn^bn * am * xm^bm
with the new shock Value V_shock, base V_base, and prefactors a, exponents b and a multiplicative combination of cross terms (term with equal cross terms are multiplied with each other, term with cross terms equal zero are added to the total value) All combined cross terms and all single terms are finally summed up.
This class contains all attributes and methods related to the following Sensitivity types:
which stands for Equity, Real Estate, Commodity, Stock and Alternative Investments. All sensitivity types assume a geometric brownian motion or brownian motion as underlying stochastic process.
In the following, all methods and attributes are explained and a code example is given.
Methods for Sensitivity object obj:
Attributes of Sensitivity objects:
For illustration see the following example: An All Country World Index (ACWI) fund with base value of 100 USD shall be modelled with both instrument setups (Linear combination of risk factor shocks and a polynomial (linear) function with two single terms. Underlying risk factors are the MSCI Emerging Market and MSCI World Index. The sensitivities to both risk factors are equal to the weights of the subindices in the ACWI index. Both risk factors are shocked during a stress scenario and the total shock values for the fund are calculated:
fprintf(' doc_instrument: Pricing Sensitivity Instrument (Polynomial Function)');
r1 = Riskfactor();
r1 = r1.set('id','MSCI_WORLD','scenario_stress',[20;-10], ...
'model','GBM','shift_type',[1;1]);
r2 = Riskfactor();
r2 = r2.set('id','MSCI_EM','scenario_stress',[10;-20], ...
'model','GBM','shift_type',[1;1] );
riskfactor_struct = struct();
riskfactor_struct(1).id = r1.id;
riskfactor_struct(1).object = r1;
riskfactor_struct(2).id = r2.id;
riskfactor_struct(2).object = r2;
s = Sensitivity();
s = s.set('id','MSCI_ACWI_ETF','sub_type','SENSI', 'currency', 'USD' , ...
'asset_class','Equity', 'value_base', 100, ...
'underlyings',cellstr(['MSCI_WORLD';'MSCI_EM']), ...
'x_coord',[0,0], ...
'y_coord',[0,0.0], ...
'z_coord',[0,0], ...
'shock_type', cellstr(['absolute';'absolute']), ...
'sensi_prefactor', [0.8,0.2], 'sensi_exponent', [1,1], ...
'sensi_cross', [0,0], 'use_value_base',true,'use_taylor_exp',false);
instrument_struct = struct();
instrument_struct(1).id = s.id;
instrument_struct(1).object = s;
s = s.calc_value('31-Dec-2016', 'base',riskfactor_struct,instrument_struct,[],[],[],2);
s.getValue('base')
s = s.calc_value('31-Dec-2016', 'stress',riskfactor_struct,instrument_struct,[],[],[],2);
s.getValue('stress')
fprintf(' doc_instrument: Pricing Sensitivity Instrument (Riskfactor linear combination)');
r1 = Riskfactor();
r1 = r1.set('id','MSCI_WORLD','scenario_stress',[20;-10], ...
'model','BM','shift_type',[1;1]);
r2 = Riskfactor();
r2 = r2.set('id','MSCI_EM','scenario_stress',[10;-20], ...
'model','BM','shift_type',[1;1] );
riskfactor_struct = struct();
riskfactor_struct(1).id = r1.id;
riskfactor_struct(1).object = r1;
riskfactor_struct(2).id = r2.id;
riskfactor_struct(2).object = r2;
s = Sensitivity();
s = s.set('id','MSCI_ACWI_ETF','sub_type','EQU', 'currency', 'USD', ...
'asset_class','Equity', 'model', 'BM', ...
'riskfactors',cellstr(['MSCI_WORLD';'MSCI_EM']), ...
'sensitivities',[0.8,0.2],'value_base',100.00);
instrument_struct = struct();
instrument_struct(1).id = s.id;
instrument_struct(1).object = s;
s = s.valuate('31-Dec-2016', 'stress', ...
instrument_struct, [], [], ...
[], [], riskfactor_struct);
s.getValue('stress')
Stress results are [118;88].
Dependencies of class:
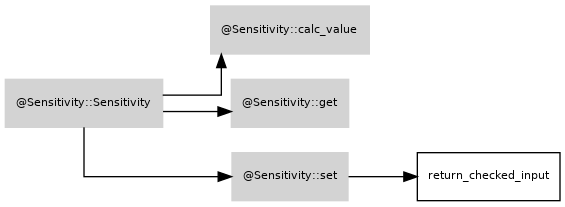
Next: Riskfactor.help, Previous: Debt.help, Up: Octave octarisk Classes [Contents][Index]